前ページまでのあらすじ
この記事では,$\tan$ の半角の公式について検討しています。
教科書や参考書に載っている公式は次の通りです。
$\tan^2\dfrac{\theta}{2}=\dfrac{1-\cos\theta}{1+\cos\theta}$ …… ③
しかし,次の図を使って検討した結果,
$\theta$ が鋭角の場合に限りますが,
$\tan^2\dfrac{\theta}{2}$ ではなく $\tan\dfrac{\theta}{2}$ を
$\sin\theta$,$\cos\theta$ の式で表すことができました。
図 5-1
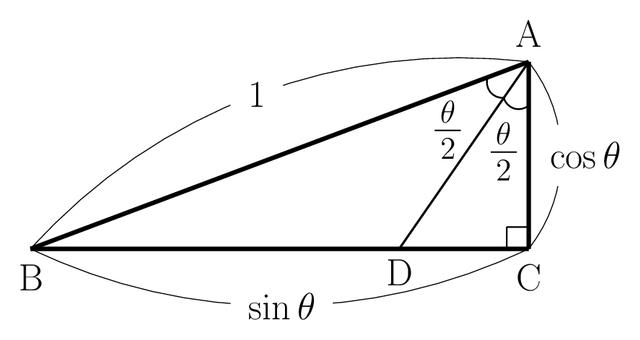
その等式は,次の通りです。
$\tan\dfrac{\theta}{2}=\dfrac{\sin\theta}{1+\cos\theta}$ ……(※1)
また,式変形による検討の結果,任意の $\theta$ について,
次の等式が成り立つことが分かりました。
$\tan\dfrac{\theta}{2}=\pm\dfrac{\sin\theta}{1+\cos\theta}$ ……(※2)
残った疑問は,次の2つです。
- $\theta$ が鈍角であるとき,図による分析は可能なのか。
- (※2)の右辺の「$\pm$」は,$\theta$ がどのような値のときに
「$+$」になり,あるいは「$-$」になるのか。
このページでは,これらの疑問について考えていきます。
ヒント3(最終) 図形的なアプローチ(任意の鈍角)
ヒントとしてはここが最終段階になります。
まだ答えそのものではないので「ヒント」と称していますが,
極めて答えに近い内容です。
図による考察($\theta$ が鈍角のとき)
$\theta$ が鈍角である場合,つまり $\dfrac{\pi}{2}<\theta<\pi$ である場合でも,
$\theta$ が鋭角のときの図 5-1と同様の図を描いて,
似たような考察を行うことは可能でしょうか。
内角の二等分線ではなく,外角の二等分線を使う
直角三角形において,直角以外の2つの内角は鋭角になります。
だから,$\theta$ が鋭角のときは,直角三角形の内角の大きさを $\theta$ とし,次の定理を利用できたわけです。
$\rm\triangle ABC$ の $\rm\angle\,A$ の二等分線と辺 $\rm BC$ の交点を $\rm D$ とするとき,
$\rm AB:AC=BD:DC$
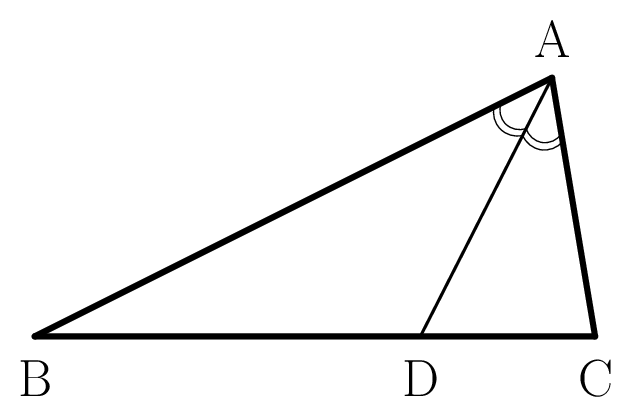
今回は,$\theta$ が鈍角の場合を考えたいので,同じ手法は使えません。
しかし,「直角三角形の直角以外の内角は鋭角」を
逆手に取ってみましょう。
内角が鋭角なら,外角は必ず鈍角になりますよね。
しかも,都合のいいことに,
上記の定理は,外角の二等分線に関するものもあります。
$\rm\triangle ABC$ の $\rm\angle\,A$ の外角の二等分線と辺 $\rm BC$ の延長線の交点を $\rm D$ とするとき,
$\rm AB:AC=BD:DC$
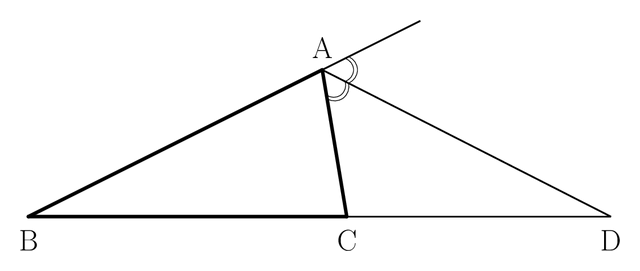
教科書にも載っているはずです。
内角の二等分線に比べてややこしいパターンとして
印象に残っている人も多いでしょう。
この定理があるとなれば,試すべきことは1つです。
直角三角形の直角以外の内角(つまり鋭角)を1つ選び,
その外角の大きさを $\theta$ とおいて,
外角の二等分線をひいてみることにしましょう。
鈍角用に改変した図
$\theta$ が鋭角のときの考察に利用した図 5-1を手直しし,
次の図図 5-2を作りました。
図 5-1(対比のため再掲)

図 5-2
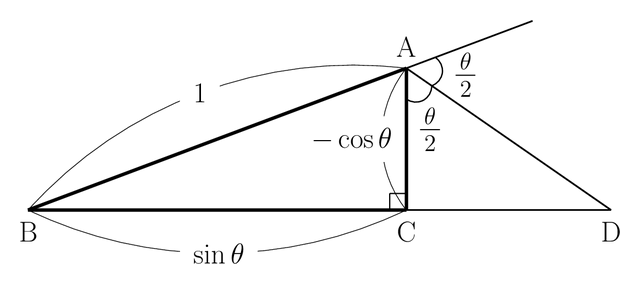
図を改変する時は,点の役割をなるべく変えない
このような図の改変では,
「同じ名前を持つ点の役割をなるべく変えないこと」
が重要なコツです。
ここでは,次のような対比になっています。
- $\rm\triangle ABC$ を,$\rm AB=1,\ \angle\,C=\dfrac{\pi}{2}$ の直角三角形とする。
- $\rm\triangle ABC$ で,$\rm\angle\,A$(内角)の大きさを $\theta$ とする。
- $\rm\triangle ABC$ で,$\rm\angle\,A$(内角)の二等分線と
辺 $\rm BC$ の交点を $\rm D$ とする。
- $\rm\triangle ABC$ を,$\rm AB=1,\ \angle\,C=\dfrac{\pi}{2}$ の直角三角形とする。
- $\rm\triangle ABC$ で,$\rm\angle\,A$ の外角の大きさを $\theta$ とする。
- $\rm\triangle ABC$ で,$\rm\angle\,A$ の外角の二等分線と
辺 $\rm BC$ の延長線の交点を $\rm D$ とする。
その効果は,すぐに明らかになります。
$\rm AB$,$\rm BC$ の長さに注意
$\rm AC$,$\rm BC$ の長さに注意しましょう。
$\rm AC=AB\cos\angle\,BAC=1\cdot\cos(\pi-\theta)=-\cos\theta$
$\rm BC=AC\sin\angle\,BAC=1\cdot\sin(\pi-\theta)=\sin\theta$
$\rm AC$ の長さは $-\cos\theta$ となっていて,
負の符号が付いているのが不自然に見えますが,
負の数になる心配はありません。
$\dfrac{\pi}{2}<\theta<\pi$ なので $\cos\theta<0$ であり,
$-\cos\theta$ はきちんと正の数になります。
$\rm BC$ の長さは,結果的には $\theta$ が鋭角のときと同じですが,
求め方は異なることに注意してください。
$\theta$ が鈍角の場合の考察
ではさっそく,$\theta$ が鈍角の場合について考えてみましょう。
$\rm AD$ が $\rm \angle\,BAC$ の外角の二等分線であることから,
$\rm AB:AC=BD:DC$
$\rm AB=1$,$\rm AC=\textcolor{#d00}{-}\cos\theta$ より,
$\rm 1:\textcolor{#d00}{(-}\cos\theta\textcolor{#d00}{)}=BD:DC$ …… (1)
$\rm BD$ と $\rm DC$ の長さを $\theta$ で表すと,
${\rm DC}={\rm AC}\tan{\rm \angle\,DAC}=\textcolor{#d00}{-}\cos\theta\tan\dfrac{\theta}{2}$
${\rm BD}={\rm BC}\textcolor{#d00}{+}{\rm DC}=\sin\theta-\cos\theta\tan\dfrac{\theta}{2}$
これらを (1) に代入すると,
$1:\textcolor{#d00}{(-}\cos\theta\textcolor{#d00}{)}=\left(\sin\theta-\cos\theta\tan\dfrac{\theta}{2}\right):\textcolor{#d00}{\left(-\vphantom{\dfrac{\theta}{2}}\right.}\cos\theta\tan\dfrac{\theta}{2}\textcolor{#d00}{\left.\vphantom{\dfrac{\theta}{2}}\right)}$
$\textcolor{#d00}{-}\cos\theta\tan\dfrac{\theta}{2}$$\vphantom{1}=\textcolor{#d00}{-}\cos\theta\left(\sin\theta-\cos\theta\tan\dfrac{\theta}{2}\right)$ …… (2)
$\textcolor{#d00}{\dfrac{\pi}{2}}<\theta<\textcolor{#d00}{\pi}$ より,$\cos\theta\;$$\neqq$$\,0$
よって,(2) の両辺を $\textcolor{#d00}{-}\cos\theta$ でわることができて,
$\tan\dfrac{\theta}{2}=\sin\theta-\cos\theta\tan\dfrac{\theta}{2}$
$\tan\dfrac{\theta}{2}+\cos\theta\tan\dfrac{\theta}{2}=\sin\theta$
$(1+\cos\theta)\tan\dfrac{\theta}{2}=\sin\theta$ …… (3)
$\textcolor{#d00}{\dfrac{\pi}{2}}<\theta<\textcolor{#d00}{\pi}$ より,$1+\cos\theta>0$
よって,(3) の両辺を $1+\cos\theta$ でわることができて,
$\tan\dfrac{\theta}{2}=\dfrac{\sin\theta}{1+\cos\theta}$ ……(※1)
$\theta$ が鋭角であるときの考え方と,よく似ていますね。
ちなみに,似ているのは考え方だけではありません。
酷似する証明
上に示した証明の文ですが,ところどころ,
不自然に赤文字が混ざっていますね。
これが何を意味しているか,お分かりになるでしょうか。
前ページで,$\theta$ が鋭角のときの証明を示しましたが,
その文章と異なる箇所が,上の赤文字なのです。
それ以外の部分(黒文字)は,一字たりとも違いません。
異なっている部分は,割合にすると,
全体のわずか数%というところでしょう。
たったこれだけの改変で,
見た目はかなり異なる図についての証明として
成立してしまうのです。
式による考察($\theta$ が鈍角のとき)
話を戻します。
図による論証をまとめると,$\theta$ が鋭角でも鈍角でも,
$\tan\dfrac{\theta}{2}=\dfrac{\sin\theta}{1+\cos\theta}$ ……(※1)
が成り立つことが分かりました。
……本当ですかね?
前ページでは,教科書に載るタイプの
$\tan$ の半角の公式(③)をもとに式変形してみると,
$\tan\dfrac{\theta}{2}=\textcolor{#ff0000}{\pm}\dfrac{\sin\theta}{1+\cos\theta}$ ……(※2)
であることが分かったのでした。
そして,この「$\pm$」について,どんな $\theta$ のときに「$+$」になり,
あるいは「$-$」になるのかが疑問として残ったのでした。
しかし,$\theta$ が鋭角でも鈍角でも,「$+$」だというのです。
それなら,一体どのような場合に,「$-$」が出てくるのでしょうか。
実を言うと,筆者は,(※2)の等式に気づいた時点では,
$\theta$ が鈍角のときに「$-$」が出てくると予想していたのです。
しかしその予想は外れ,鈍角でも「$+$」でした。
強いて言うなら,$\theta$ は一般角なので, $\pi$($180^\circ$)より大きい角や,
$0$($0^\circ$)より小さい角(負の角)なんてものも,
考えに入れる必要があります。
その広い範囲のどこかで,「$-$」が出てくるのでしょうか。
常に「+」である可能性
筆者は,ここまで考えてようやく,(※2)の解釈に,
次の3つの可能性があることに気がつきました。
- $\theta$ の値によって,「$+$」になったり「$-$」になったりする。
- 実は常に「$+$」である。
- 実は常に「$-$」である。
筆者は,(A) の可能性しか想定していなかったわけです。
でも,よく考えてみると,(※2)はもともと,
次の等式から導いたものでした。
$\tan^2\dfrac{\theta}{2}=\left(\dfrac{\sin\theta}{1+\cos\theta}\right)^2$ ……(*)
これを,「$\pm$」を使って(※2)の形に書き直したのが,
あまりよくなかったかもしれません。
(※2) の形だと,$\theta$ の値によって,
「$+$」になったり「$-$」になったりするものだと思いがちです。
しかし,仮に (B) や (C) が真実であるとしても,
(*)は問題なく成立しますからね。
完全に盲点になっていました。
(※1)の証明に挑戦
$\theta$ の値によらず,(※2)の「$+$」,
つまり(※1)が成立するかもしれない。
ならばいっそのこと,(※1)が常に成り立つことの証明に
挑戦してみましょうか。
実は成り立たないのだとしても,
「$+$」になる場合と「$-$」になる場合を見分けるのに,
役に立つかもしれません。
証明の方針がまだ思い浮かんでいない人は,
ぜひ,次ページを見る前に挑戦してみてください。
練習問題として,それほど難しくないレベルです。
証明しやすくするために
(※1)を証明しようとすると,$\dfrac{\theta}{2}$ が多数出てきて,
煩雑なことになりそうです。
なので,次の等式を証明した上で,
$\theta$ を $\dfrac{\theta}{2}$ に置きかえて(※1)を得るという方針で
考えるとよいでしょう。
$\tan\theta=\dfrac{\sin 2\theta}{1+\cos 2\theta}$
次ページの内容
はたして,半角の公式として,
(※1)を採用してもよいのかどうか。
次ページで,いよいよその問題を決着させます。