前ページまでのあらすじ
$\,\tan\;$の半角の公式について考えるための準備として,
$\,\tan 22.5^\circ$ の値を図形的に求める方法を紹介しました。
ここでは,前ページの図の $45^\circ$ を $\theta$ に,
$22.5^\circ$ を $\dfrac{\theta}{2}$ に置き換えて,
同じ考え方がどこまで通用するかを試してみます。
ヒント2 図形的なアプローチ(任意の鋭角)
ヒントと称していますが,
ここから急速に答えに近づいていきます。
なるべく自力で考えたいとお考えの方はご注意ください。
前ページの考察は,直角二等辺三角形だったからできたわけではない
前ページでは,次の図をもとに,$\tan 22.5^\circ$ の値を求めました。
図 4-1
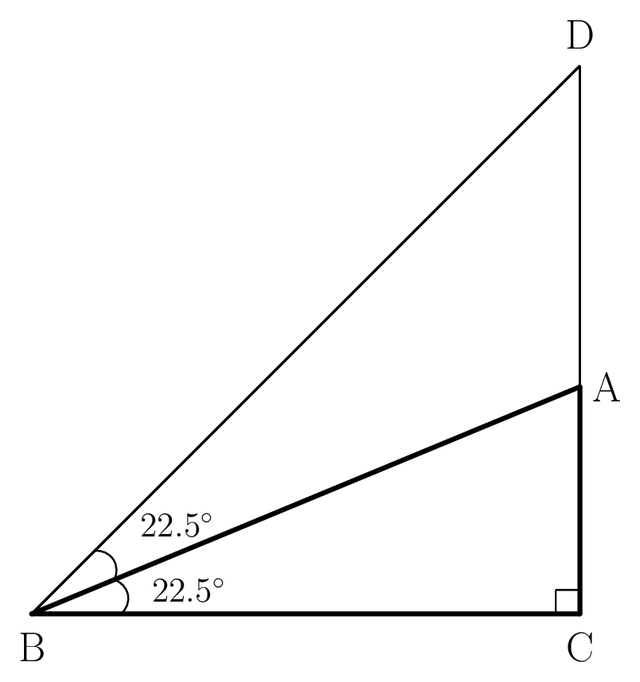
その計算過程は,別に,$\rm BC=CD$ だったから
可能だったわけではないですね。
$\rm \triangle DBC$ の3辺の長さがすべて分かっている必要はありますが,
それらの値を比例式に代入して解いただけであり,
$\rm BC=CD$ であることを利用したわけではありません。
となると,$45^\circ$ と $22.5^\circ$ という角でなくても,
似たような考え方がかなりの程度通用するのではないかと
期待できるわけです。
一般的な角 $\theta$ を使った図
次の図は,前ページの直角二等辺三角形の図を描きかえて,
大きさが $\theta$ の角を2等分するようにしたものです。
図 4-2
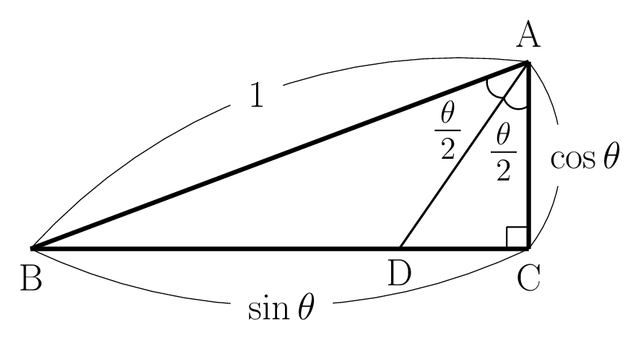
この図の特徴を整理しておきます。
- $\rm \triangle ABC$ は,$\rm \angle\,C=\dfrac{\pi}{2}(=90^\circ)$ の直角三角形。
- $\rm \angle\,BAC=\theta$ であり,$\rm AD$ は $\rm \angle\,BAC$ の
二等分線になっている。
この図に現れる線分の長さは
この図の通りでなくても構わないのですが,
ここでは直角三角形 $\rm ABC$ の斜辺 $\rm AB$ の長さを $1$ としました。
このとき,$\rm AC=\cos\theta$,$\rm BC=\sin\theta$ となることは大丈夫ですね。
図から導ける公式(のようなもの)
$\rm AD$ が $\rm \angle\,BAC$ の二等分線であることから,
$\rm AB:AC=BD:DC$
$\rm AB=1$,$\rm AC=\cos\theta$ より,
$\rm 1:\cos\theta=BD:DC$ …… (1)
$\rm BD$ と $\rm DC$ の長さを $\theta$ で表すと,
${\rm DC}={\rm AC}\tan{\rm \angle\,DAC}=\cos\theta\tan\dfrac{\theta}{2}$
${\rm BD}={\rm BC}-{\rm DC}=\sin\theta-\cos\theta\tan\dfrac{\theta}{2}$
これらを (1) に代入すると,
$1:\cos\theta=\left(\sin\theta-\cos\theta\tan\dfrac{\theta}{2}\right):\cos\theta\tan\dfrac{\theta}{2}$
$\cos\theta\tan\dfrac{\theta}{2}=\cos\theta\left(\sin\theta-\cos\theta\tan\dfrac{\theta}{2}\right)$ …… (2)
$0<\theta<\dfrac{\pi}{2}$ より,$\cos\theta\;$$\neqq$$\,0$
よって,(2)の両辺を $\cos\theta$ でわることができて,
$\tan\dfrac{\theta}{2}=\sin\theta-\cos\theta\tan\dfrac{\theta}{2}$
$\tan\dfrac{\theta}{2}+\cos\theta\tan\dfrac{\theta}{2}=\sin\theta$
$(1+\cos\theta)\tan\dfrac{\theta}{2}=\sin\theta$ …… (3)
$0<\theta<\dfrac{\pi}{2}$ より,$1+\cos\theta>0$
よって,(3)の両辺を $1+\cos\theta$ でわることができて,
$\tan\dfrac{\theta}{2}=\dfrac{\sin\theta}{1+\cos\theta}$ ……(※1)
見事に,$\tan\dfrac{\theta}{2}$ を $\sin\theta$ と $\cos\theta$ で表す式が出てきました。
半角の公式として求められる要件は,
$\theta$ についての三角関数の値から,
$\dfrac{\theta}{2}$ についての三角関数の値が求められること
です。
(※1)は,その要件を満たしており,
半角の公式として使えそうな等式です。
そして何より,
教科書などに載る半角の公式(下記の③)とは違って,
$\tan\dfrac{\theta}{2}$ の値そのものを求められる式であることが強みです。
$\tan^2\dfrac{\theta}{2}=\dfrac{1-\cos\theta}{1+\cos\theta}$ …… ③
公式③は,できれば $\tan\dfrac{\theta}{2}$ の値が知りたいのに,
$\tan^2\dfrac{\theta}{2}$ の値しか求められないという意味で,
扱いにくいですから。
ここで導いた公式で十分と判断するのはまだ早い
では,教科書や参考書に載っている公式③は捨てて,
(※1)を公式として採用するということでよいでしょうか?
それはいけません。
少なくとも,まだだめです。
ここで導いた(※1)が,どんな角 $\theta$ でも成り立つかどうかを,まだ検討していないからです。
そもそも,この論証に使った図 4-2自体が,$\theta$ が鋭角の場合,
つまり $0<\theta<\dfrac{\pi}{2}$ の場合にしか描けない図ですから。
そして実際,上の論証の中で,
「$0<\theta<\dfrac{\pi}{2}$ より,」という文言が2回出てきています。
要するに,この論証は $\theta$ が鋭角である場合に限って有効
だったわけです。
この等式(※1)は,$0<\theta<\dfrac{\pi}{2}$ の範囲では
成り立つことが分かったので,その範囲内にある $\theta$ に限れば,
公式として使っても問題ないと言えます。
しかし,$\theta$ がその範囲にない場合は,(※1)が成り立たず
別の等式が成り立つといった可能性も大いにあります。
$\theta$ が鈍角の場合について,同様の図による分析は可能?
「$\theta$ が鋭角なら成り立つ」と言われたら,
「なら鈍角ではどうなんだ」と思う人が多いでしょう。
そして,鈍角のケースも図で,
しかも鋭角のときと似たような図で分析できないかと
考えるのも,自然な思考だと思います。
しかし,内角の1つが鈍角である直角三角形 $\rm ABC$
などというものは存在しません。
よって,鈍角のケースを図で分析することは不可能…
なのでしょうか?
ここは,興味のある人には少し考えてもらいたいポイントなので,
答えは次のページに譲ることにします。
式変形によるアプローチ
2つの等式が出てきたが,どっちが正しい?
ひとまず,$0<\theta<\dfrac{\pi}{2}$ という狭い範囲ではありますが,
$\theta$ の値によらず成り立つ式(※1)が見つかりました。
しかし,$\tan\dfrac{\theta}{2}$ の値を求める式の表現が
1通りに決まらないことについては,
不自然さや不安を感じる人も多いでしょう。
教科書に載るタイプの半角の公式③と(※1)は,
一体どっちが正しいのかというわけです。
そもそも,(※1)の右辺を2乗したら,
③の右辺と一致するのでしょうか?
\begin{eqnarray*}
\left(\dfrac{\sin\theta}{1+\cos\theta}\right)^2&=&\dfrac{\sin^2\theta}{(1+\cos\theta)^2}\\
&=&\dfrac{1-\cos^2\theta}{(1+\cos\theta)^2}\vphantom{\Large\dfrac{1}{1}}\\
&=&\dfrac{(1+\cos\theta)(1-\cos\theta)}{(1+\cos\theta)^2}\vphantom{\Large\dfrac{1}{1}}\\
&=&\dfrac{1-\cos\theta}{1+\cos\theta}\vphantom{\Large\dfrac{1}{1}}
\end{eqnarray*}
なるほど,きっちり $\tan^2\dfrac{\theta}{2}$ の式と一致するんですね。
このように,三角関数では,一見すると全く異なる式が
実は恒等的に等しいということがよくあります。
従って,③と(※1)のどちらも正しいという可能性は十分あり,既に矛盾が生じているのではないかと怪しむ理由は
特にないと言えます。
この式変形を逆にたどると…
この式変形を逆にたどると,次のようになります。
\begin{eqnarray*}
\tan^2\dfrac{\theta}{2}&=&\dfrac{1-\cos\theta}{1+\cos\theta}\\
&=&\dfrac{(1-\cos\theta)(1+\cos\theta)}{(1+\cos\theta)^2}\vphantom{\Large\dfrac{1}{1}}\\
&=&\dfrac{1-\cos^2\theta}{(1+\cos\theta)^2}\vphantom{\Large\dfrac{1}{1}}\\ &=&\dfrac{\sin^2\theta}{(1+\cos\theta)^2}\vphantom{\Large\dfrac{1}{1}}\\
&=&\left(\dfrac{\sin\theta}{1+\cos\theta}\right)^2\vphantom{\Large\dfrac{1}{1}}
\end{eqnarray*}
$\tan$ の半角の公式③を見慣れている人でも,
その右辺の $\dfrac{1-\cos\theta}{1+\cos\theta}$ を変形すると,
ある式の2乗の形で表せることには,
気づいていないことが多いのではないかと思います。
何の脈絡もなく分子と分母に $(1+\cos\theta)$ をかけているところが,
少しトリッキーで気づきにくいですからね。
普通であれば,まず試すことのない式変形と言えるでしょう。
しかし,これは重要な情報です。
式変形の結果を改めて見てみましょう。
すなわち,$\tan\dfrac{\theta}{2}$ と $\dfrac{\sin\theta}{1+\cos\theta}$ は,
それぞれの2乗が互いに一致すると言うのです。
ただし,
と判断するのは早合点ですよ。
正しくは次の通りです。
プラスマイナス($\pm$)が付くんですね。
プラスマイナス(±)の解釈
(※2)は,「$\pm$」が付いたとはいえ,
$\tan^2$ ではなく $\tan$ の値を直接求められる式になっています。
その意味では,$\tan$ の半角の公式(①)より
使いやすい式になっていると言えるのではないかと思います。
ただ,$\theta$ がどのような値のときに「$+$」になり,
あるいは「$-$」になるのかは,
可能ならばはっきりさせておきたいところです。
次ページの内容
このページでは,次の2点について疑問が残りました。
- $\theta$ が鈍角であるとき,図による分析は可能なのか。
- (※2)の右辺の「$\pm$」は,$\theta$ がどのような値のときに
「$+$」になり,あるいは「$-$」になるのか。
次ページでは,これらの点について調べていきます。