【課題学習のテーマ】半角の公式（tan）の別の形を見つける

前ページまでのあらすじ

本記事の主題は$\;\tan\;$の半角の公式を深追いすることですが，
手始めに，よく半角の公式で求められる
$\sin 22.5^\circ$，$\cos 22.5^\circ$，$\tan 22.5^\circ$ の値を見比べました。

$\sin 22.5^\circ=\dfrac{\sqrt{2-\sqrt{2}}}{2}$

$\cos 22.5^\circ=\dfrac{\sqrt{2+\sqrt{2}}}{2}$

$\tan 22.5^\circ=\sqrt{2}-1 \vphantom{\sqrt{\dfrac{2+\sqrt{2}}{4}}}$

$\tan 22.5^\circ$ の値が，
他の２つに比べてやけにシンプルですが，
これは偶然なのでしょうか。

一方で，図形的なアプローチも考えてみたいと思います。

図 3-1

$22.5^\circ$ の三角比と聞けば
誰でも思い浮かべるであろうこの図には，
$45^\circ$ の角が出てきません。

半角の公式について図形的に考えるなら，
$22.5^\circ$ の２倍にあたる $45^\circ$ の角が現れる図を
使う必要があるでしょう。

どうしたらよいでしょうか。

ヒント１　図形的なアプローチ（特定の角）

図の中に $45^\circ$ の角を含めてみる

筆者が利用したのは次の図です。

図 3-2

図 3-1の上の方に線を描かき加えた形ですね。

この図のいいところを挙げてみます。

$45^\circ$ の角を持つ直角三角形が含まれている。
そのおかげで，$\rm \cos 45^\circ=\dfrac{BC}{DB} \vphantom{\Large\dfrac{1}{1}}$ など，
$45^\circ$ の三角比が線分の長さで表せる。
三角形の内角の二等分線が現れている。

三角形の内角の二等分線といえば，次の定理がありますね。

定理　三角形の内角の二等分線と線分の比

$\rm\triangle ABC$ の $\rm\angle\,A$ の二等分線と辺 $\rm BC$ の交点を $\rm D$ とするとき，

　　$\rm AB:AC=BD:DC$

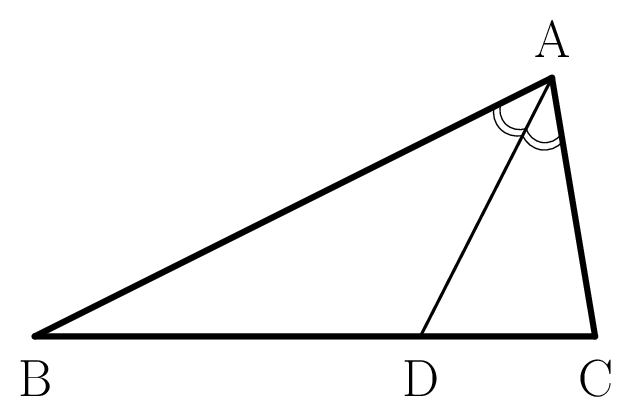
この定理の比例式を図 3-2に適用すると，
何かが導けそうな気がしませんか。

図を使って $22.5^\circ$ の三角比を考えてみる

図 3-2において，$\rm BC=CD=1$，$\rm BD=\sqrt{2}$ であるとします。

$\rm BA$ は $\rm \angle\,DBC$ の二等分線だから，

　$\rm BC:BD=CA:AD$ …… (1)

$\rm CA$，$\rm AD$ の長さは次の通り。

　$\rm CA=BC\cdot\tan 22.5^\circ=1\cdot\tan 22.5^\circ=\tan 22.5^\circ$
　$\rm AD=CD-CA=1-\tan 22.5^\circ$

したがって，(1)より，

　$1:\sqrt{2}=\tan 22.5^\circ:(1-\tan 22.5^\circ)$

　$1-\tan 22.5^\circ=\sqrt{2}\tan 22.5^\circ$

　$(\sqrt{2}+1)\tan 22.5^\circ=1$

\begin{eqnarray*}
\tan 22.5^\circ&=&\dfrac{1}{\sqrt{2}+1}\\
&=&\dfrac{\sqrt{2}-1}{(\sqrt{2}+1)(\sqrt{2}-1)} \vphantom{\LARGE\dfrac{1}{1}}\\
&=&\dfrac{\sqrt{2}-1}{2-1} \vphantom{\LARGE\dfrac{1}{1}}\\
&=&\sqrt{2}-1 \vphantom{\LARGE 1}
\end{eqnarray*}

はい，$\tan 22.5^\circ$ が求められました。
感覚的には，「$\tan 22.5^\circ$」を変数と見て，
１次方程式を解いただけです。

ずいぶんスムーズに求められたと思いません？

半角の公式で求めた時は，

$\tan^2 22.5^\circ$ を求めて，$\tan 22.5^\circ>0$ だから ……

などと，まどろっこしいことをしていたのに。

この方法で $\sin 22.5^\circ$ や $\cos 22.5^\circ$ の値を求めるのは難しそう

筆者が試した限りでは，図 3-2を利用して
$\sin 22.5^\circ$ や $\cos 22.5^\circ$ の値を求めようとしても，
$\tan 22.5^\circ$ ほど手軽には求められませんでした。

$\sin 22.5^\circ$ や $\cos 22.5^\circ$ の値は，前ページで示した通り，
二重根号を使わないと表せません。

そんな複雑な値を，上記の $\tan 22.5^\circ$ と同じくらいに
すんなりと求めるのは，ちょっと無理な気がします。

ですので，ここからは $\tan$ に的まとを絞しぼって考えていきます。

$\tan 22.5^\circ$ は他の図からも求められる

$\tan 22.5^\circ\;$の値は，次の図からも求められます。

この図を念頭に本記事のテーマについて考えても，
本記事と同等のところまで迫れるようです。ℹ️️

興味のある方は考えてみてください。

角が $22.5^\circ$ だったからできたことなのか

$\tan$ の値だけがすんなり求められたことで，
$\tan$ には何か秘密があるのではという疑惑が
深まった気がしますが，
あくまで，$22.5^\circ$ という１つの角についてのみ
調べた結果です。

しかも，図を加工すると直角二等辺三角形が現れるという，
かなり特別な角です。

となると，次に気になるのは，
$22.5^\circ$ 以外の角についても，
上記と同じような考え方が通用するかどうかです。

そこで，次の方向で考察を進めてみたいと思います。

図 3-2と同じような図を，
一般的な角 $\theta$ について描かいてみる。

すなわち，図中の「$22.5^\circ$」を「$\,\dfrac{\theta}{2}\,$」に置き換えた図にする。

その図を利用することにより，$\tan\dfrac{\theta}{2}$ を，
$\sin\theta$，$\cos\theta$，$\tan\theta$ のどれか（複数でもよい）を
使った式で表せるかどうかを調べる。

次ページの内容

一般的な角 $\theta$ についての図を示しつつ，分析を進めていきます。
また，その図を使うときに注意すべきことを指摘します。

その図から一定の結論が得られたら，
式の変形の観点から，$\tan$ の半角の公式について考えます。