【課題学習のテーマ】半角の公式（tan）の別の形を見つける

前ページのあらすじ

高校数学Ⅱの【三角関数】で扱われる「半角の公式」は，
以下の３つがあります。

半角の公式 $\left(\,\sin\rbfrac(\theta)(2)\;,\;\cos\rbfrac(\theta)(2)\,\right)$

$\sin^2\dfrac{\theta}{2}=\dfrac{1-\cos\theta}{2}$ …… ①

$\cos^2\dfrac{\theta}{2}=\dfrac{1+\cos\theta}{2}$ …… ②

（教科書に載るタイプの）半角の公式 $\left(\,\tan\rbfrac(\theta)(2)\,\right)$

$\tan^2\dfrac{\theta}{2}=\dfrac{1-\cos\theta}{1+\cos\theta}$ …… ③

ある時，筆者は半角の公式を
図形的に導く方法を考えていたのですが，
その過程で，$\tan\dfrac{\theta}{2}$ について，
③とは別の形の等式が出てきました。ℹ️️

しかも，③よりシンプルで，
公式として使いやすそうな形でです。

それを公式として使っても問題ないのか，
深追いしてみたくなりました。

考えるきっかけ

このページでは，筆者が半角の公式を図形的に導こうと
思ったきっかけをお話ししていこうと思います。

典型的な問題例

筆者は，ものすごく久しぶりに，
次の問題を解きました。

半角の公式（①～③）を使う典型的な問題です。

もちろん，答えも全く記憶にない状態でした。

例題１

$\sin 22.5^\circ$，$\cos 22.5^\circ$，$\tan 22.5^\circ$ を求めなさい。

解答例１

公式②，③より，

\[
\begin{eqnarray*}
\sin^2 22.5^\circ&=&\dfrac{1-\cos 45^\circ}{2}\\[0.6em]
&=&\dfrac{1-\dfrac{\sqrt{2}}{2}}{2}\\[0.6em]
&=&\dfrac{2-\sqrt{2}}{4}
\end{eqnarray*}
\]

\[
\begin{eqnarray*}
\cos^2 22.5^\circ&=&\dfrac{1+\cos 45^\circ}{2}\\[0.6em]
&=&\dfrac{1+\dfrac{\sqrt{2}}{2}}{2}\\[0.6em]
&=&\dfrac{2+\sqrt{2}}{4}
\end{eqnarray*}
\]

$0^\circ<22.5^\circ<90^\circ$ であるから，$\sin 22.5^\circ>0$，$\cos 22.5^\circ>0$

よって，

　$\sin 22.5^\circ=\sqrt{\dfrac{2-\sqrt{2}}{4}}=\dfrac{\sqrt{2-\sqrt{2}}}{2}$

　$\cos 22.5^\circ=\sqrt{\dfrac{2+\sqrt{2}}{4}}=\dfrac{\sqrt{2+\sqrt{2}}}{2}$

また，

\[\begin{eqnarray*}
\tan 22.5^\circ&=&\dfrac{\sin 22.5^\circ}{\cos 22.5^\circ}\\[0.6em]
&=&\dfrac{\sqrt{2-\sqrt{2}}}{\sqrt{2+\sqrt{2}}}\\[0.6em]
&=&\sqrt{\dfrac{(2-\sqrt{2})^2}{(2+\sqrt{2})(2-\sqrt{2})}}\\[0.6em]
&=&\sqrt{\dfrac{(2-\sqrt{2})^2}{4-2}}\\[0.6em]
&=&\dfrac{2-\sqrt{2}}{\sqrt{2}}\\[0.6em]
&=&\dfrac{\sqrt{2}\,(\sqrt{2}-1)}{\sqrt{2}}\\[0.6em]
&=&\sqrt{2}-1
\end{eqnarray*}
\]

…おや？
この記事の主役であるはずの公式③が出てきませんでした。

いや，いきなり$\tan 22.5^\circ$を求めるのであれば
使ったんですけどね。

$\sin 22.5^\circ$ と $\cos 22.5^\circ$ の値がわかり，
それらから $\tan 22.5^\circ$ を求められる状況になったもので。
わざわざ$\tan^2 22.5^\circ$を求める公式を使う気に
なりにくかったのです。

使うとすれば次のようになります。

解答例２

公式③より，

\[
\begin{eqnarray*}
\tan^2 22.5^\circ&=&\dfrac{1-\cos 45^\circ}{1+\cos 45^\circ}\\[0.6em]
&=&\dfrac{1-\dfrac{\sqrt{2}}{2}}{1+\dfrac{\sqrt{2}}{2}}\\[0.6em]
&=&\dfrac{2-\sqrt{2}}{2+\sqrt{2}}\\[0.6em]
&=&\dfrac{(2-\sqrt{2})^2}{(2+\sqrt{2})(2-\sqrt{2})}\\[0.6em]
&=&\dfrac{(2-\sqrt{2})^2}{4-2}\\[0.6em]
&=&\dfrac{(2-\sqrt{2})^2}{2}\\[0.6em]
\end{eqnarray*}
\]

$0^\circ<22.5^\circ<90$ であるから，$\tan 22.5^\circ>0$

よって，

\[\begin{eqnarray*}
\tan 22.5^\circ&=&\sqrt{\dfrac{(2-\sqrt{2})^2}{2}}\\[0.6em]
&=& {\rm（解答例１と似た計算なので中略）}\\[0.4em]
&=&\sqrt{2}-1
\end{eqnarray*}
\]

$\;\sin 22.5^\circ$，$\cos 22.5^\circ$，$\tan 22.5^\circ\;$の値を見比べる

さて，この例題では，$\sin 22.5^\circ$，$\cos 22.5^\circ$，$\tan 22.5^\circ$ という
３つの値を求めました。

$\sin 22.5^\circ=\dfrac{\sqrt{2-\sqrt{2}}}{2}$

$\cos 22.5^\circ=\dfrac{\sqrt{2+\sqrt{2}}}{2}$

$\tan 22.5^\circ=\sqrt{2}-1 \vphantom{\sqrt{\dfrac{2+\sqrt{2}}{4}}}$

これらの値を見比べてみて，どう思いますか。
筆者は，次のような感想を持ちました。

$\sin$ と $\cos$ はかなり複雑で，
二重根号まで残っているのに，
$\tan$ は随分ずいぶんシンプルになるんだな。

上の例題は多くの教科書に載のっているでしょうから，
実際に解いて同じ感想を持った高校生は，
少なくないのではないかと思います。

この時，筆者の頭には，次の疑問が引っかかりました。

$22.5^\circ$ という角度について，
$\tan$ の値が $\sin$ や $\cos$ に比べて
シンプルになったのは偶然なのだろうか。

ちょっとだけネタばらし（疑問に対する答え）

この疑問に対する結論としては，
$\,\tan 22.5^\circ$ の値が $\sin 22.5^\circ$ や $\cos 22.5^\circ$ に比べて
シンプルになったのは「必然であった」となります。

この例題くらいなら，図形的に解決できそうな気も

ちなみに筆者は，この例題を解いている間に，

$45^\circ$ の角と $22.5^\circ$ の角が
両方出てくる図を使うことで，
$22.5^\circ$ の三角比を図形的に求められるのでは？

と思うようになっていました。

$22.5^\circ$ の三角比について考えるなら，
多くの人がまず次のような図を思い浮かべるでしょう。

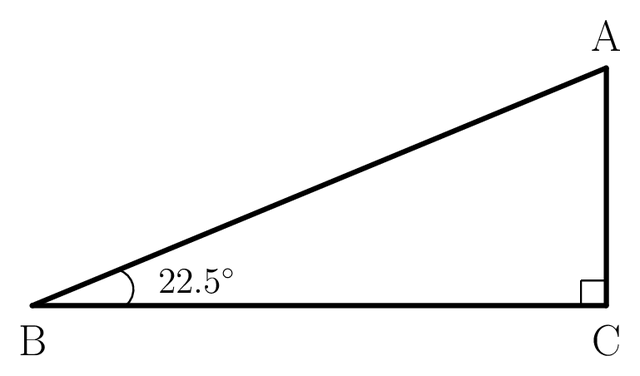
しかし，この図には，$45^\circ$ の角が出てきません。

この図に手を加えて，$22.5^\circ$ の三角比と
$45^\circ$ の三角比の関係が
考えられるようにしたいのですが，
どのような図にするとよいと思いますか。

次ページの内容

筆者が思い浮かべた図を明らかにした上で，
その図を利用して $22.5^\circ$ の三角比を
求める方法を考えてみます。