前ページまでのあらすじ
当記事独自のＡＩ数学推論能力検証を進めています。
問３まで終了し，残り２問です。
世間で広く使われているチャットＡＩの
数学推論能力の実態が
だんだん分かってきたところかと思います。
以下に述べる問４は，
人間ならほとんど間違えそうにないことを
なぜかＡＩがかなりの確率で
間違える事例になりました。
問４
質問内容
問４は，連続関数のグラフに関する質問です。
２つの連続な単調減少関数のグラフの共有点は，
最大でも１つであるという主張は正しいですか？
用語について
関数の「単調減少」は高校数学Ⅱ，
関数の「連続」は高校数学Ⅲで学ぶ内容ですが，
深い理解が必要な質問ではありません。
この程度の理解で十分ですので，極端なことを言えば，
この質問に正しく答えるだけなら
中学生でも可能かもしれません。
質問の意味
例えば，次の図をご覧ください。
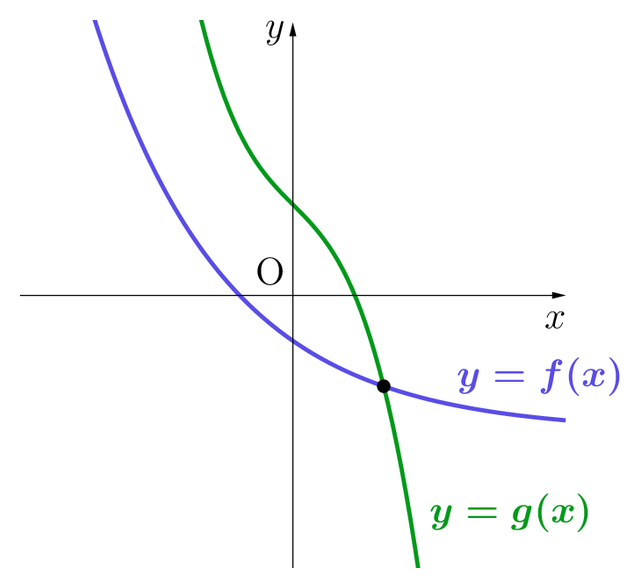
座標平面上に２つの曲線がありますね。
これらが関数の曲線です。
どちらのグラフも，途切れている部分はなく，
どの部分においても右下がりなので，
連続な単調減少関数のグラフです。
そして，この図を見る限り，
２つの曲線は１点で交わっていますね。
つまり，共有点が１つということです。
そこで，問４の質問です。
小難しい質問に見えますが，上記のことを押さえれば，
中学生でも十分考えられる問題だと思います。
質問の意図
この質問の詳しい意図は後述のサブ記事に譲りますが，
はっきり言って愚問です。
それなりに数学に慣れている人が落ち着いて考えれば，
まず間違えないのではないでしょうか。
ＡＩたちがこんな愚問を投げられた際は，
正確かつ簡潔に片付けてほしいところです。
しかし意外にも，ＡＩたちの判断は分かれたのです。
詳しくはサブ記事で
問４に関する説明やＡＩからの回答，
および採点結果については，
下記のサブ記事をご覧ください。
問４ 採点結果
各ＡＩの得点
問４における各ＡＩの得点は
次のようになりました。（※１０点満点）
参加ＡＩ名 問４の得点 ChatGPT-T １０点 DeepSeek-T １０点 MathGPT-T １０点 Gemini-T ９点 Perplexity-T ９点 Grok-T ８点 Copilot-N ５.５点 Claude-N ４点 Copilot-T ３点 Gemini-N ３点 Grok-N ３点 DeepSeek-N ２.５点 MathGPT-N ２.５点 Perplexity-N ２点 ChatGPT-N １.５点
「サービス名-N」は熟考機能オフ，
「サービス名-T」は熟考機能オンです。
より正確な意味については，
当記事の２ページ目をご覧ください。
平均点
問４の平均点は次の通りです。
| 全参加ＡＩの平均点 | 5.53 点 |
| 高速モデル (-N) の平均点 | 3.00 点 |
| 熟考モデル (-T) の平均点 | 8.43 点 |
問４ 総評・所感
人間には簡単なのにＡＩには難しい？
問４の主張が「正しくない」という正解を
１回目の回答で示したのは，
全参加ＡＩ（１５モデル）のうち６モデルありましたが，
その全てが熟考モデル (-T) でした。
つまり高速モデル (-N) は全滅だったわけです。
高速モデルの中で唯一反例を示してくれた Copilot-N も，
「狭義単調減少関数に限れば正しい」と
不正確なことを述べていました。
人間にとっては当たり前すぎて
改めて問うほどの問題でもないと思うのですが，
ＡＩにとっても当たり前とは限らないという
好例かと思います。
高速モデルと熟考モデルで差が大きかった
高速モデル (-N) が全滅する一方，
熟考モデル (-T) は Copilot-T が不覚をとっただけで，
残りは正解しました。
ゆえに，高速モデルと熟考モデルの差が
非常に大きい結果となりました。
よく考えて答えれば正しい結論を導きやすい
問いだったということでしょうか。
次ページの内容
この検証も，いよいよ最後の問いとなります。
次の問５は，筆者が自分で考えた問題の中では
かなり気に入っているものです。
正解が直感とは異なると感じる人も
多そうな問題だと思っているのですが，
ＡＩたちはどのように対処するのでしょうか。