前ページまでのあらすじ
前ページで,筆者が勝手に巻き込んだ
チャットAIたちの数学推論能力の検証を始めました。
問1は2次式の因数分解に関する
極めて基本的な質問でしたが,
広く使われているAIでも取りこぼす場面が
少なからず見られました。
このページでは,引き続き,
問2による検証を行います。
問2
質問内容
今度は,知らない人が解くには
やや難しいかもしれない図形問題です。
$\rm\triangle ABC\;$の角$\;\rm A\;$の二等分線と辺$\;\rm BC\;$の交点を$\;\rm D\;$とします。
このとき,$\rm BD=CD\;$となるならば,
$\rm\triangle ABC\;$は二等辺三角形であると言えますか。
答えがイエスなら証明を,ノーなら反例を示してください。
ただし,日本の中学数学で理解できる範囲でお願いします。
入力文:
△ABCの角Aの二等分線と辺BCの交点をDとします。
このとき,BD=CDとなるならば,
△ABCは二等辺三角形であると言えますか。
答えがイエスなら証明を,ノーなら反例を示してください。
ただし,日本の中学数学で理解できる範囲でお願いします。
この質問の状況を図に表すと,次のようになります。
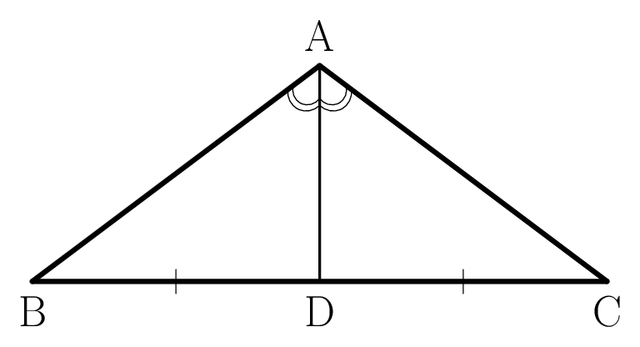
二等辺三角形かどうか分かっていない$\;\rm\triangle ABC\;$において,
$\;\rm\angle\,A\;$の二等分線と辺$\;\rm BC\;$の交点をとってみると,
辺$\;\rm BC\;$の中点になりましたと。
このとき,実は$\;\rm\triangle ABC\;$は二等辺三角形であると
断言してよいかという問題です。
質問の意図
安易に △ABD≡△ACD を示そうとしてもうまくいかない

この図を見れば,まずは誰もが,
$\;\rm\triangle ABD\equiv\triangle ACD\;$の証明を試みるところでしょう。
仮定より$\;\rm BD=CD\;$かつ$\;\rm\angle\,BAD=\angle\,CAD\;$,
共通だから$\;\rm AD=AD\;$。
しかしこれでは,
「2組の辺とその間の角がそれぞれ等しい」とは
言えないですね。
$\;\rm\angle\,BAD\;$は$\;\rm AD\;$と$\;\rm BD\;$の間の角ではありませんし,
$\;\rm\angle\,CAD\;$も$\;\rm AD\;$と$\;\rm CD\;$の間の角ではありませんから。
このもどかしい状況をかいくぐって,
どのように$\;\rm AB=AC\;$を証明するか。
あるいは,$\rm\triangle ABC\;$が二等辺三角形に
ならないことがあるのか。
この問2は,そういう問題です。
詳しくはサブ記事で
問2に関する説明やAIからの回答,
および採点結果については,
下記のサブ記事をご覧ください。
問2 採点結果
各AIの得点
問2における各AIの得点は
次のようになりました。(※10点満点)
参加AI名 問2の得点 MathGPT-T 10点 Gemini-T 9.5点 DeepSeek-N 7点 Grok-T 6点 MathGPT-N 6点 ChatGPT-T 4点 Gemini-N 2.5点 Copilot-T 2点 Copilot-N 1.5点 Perplexity-N 1.5点 Perplexity-T 1.5点 ChatGPT-N 0.5点 Grok-N 0.5点 DeepSeek-T 0.5点 Claude-N 0点
「サービス名-N」は熟考機能オフ,
「サービス名-T」は熟考機能オンです。
より正確な意味については,
当記事の2ページ目をご覧ください。
平均点
問2の平均点は次の通りです。
| 全参加AIの平均点 | 3.53 点 |
| 高速モデル (-N) の平均点 | 2.44 点 |
| 熟考モデル (-T) の平均点 | 4.79 点 |
問2 総評・所感
安直な誤りが多すぎる
平均点自体もだいぶ悪いように見えますが,
何と言ってもひどいのは,
安易に$\;\rm\triangle ABD\equiv\triangle ACD\;$が示せたと
主張するAIが続出したことです。
全参加AI(15モデル)のうち,7モデルもありました。
それを含めて,一度でも誤った証明を
正しいと主張したのは実に10モデル,
全体の3分の2に上りました。
筆者はこの問2で,AIたちがだまされないかを
試すつもりはなかったのです。
直接$\;\rm\triangle ABD\equiv\triangle ACD\;$を示せないのは分かりきっているけれども,
その難点をかいくぐって正解にたどり着けるかどうか,
かつ正確な推論を展開できるかを見るつもりでした。
しかし,AIたちには失礼ながら,
あまりの惨状に閉口してしまったというのが本音です。
一方,一度も誤った証明を提示せず,
中学生でも理解できる正しい証明を示したのは
3モデル。
一度も誤った証明を提示せず,
中学数学の範囲では難しいと判断したのが
2モデルでした。
分からないなら分からないと言ってくれないと困る
この問題は,解けなくてもよいのです。
人間の数学指導員でも,
知らなければ簡単には即答できない問題だと思います。
筆者は,(甘いと言う人もいるかもしれませんが)
この問題が解けない人に数学の指導員は
務まらないとは思いません。
問2の内容は,中学数学で
必ず指導するものではありませんから。
もちろん解けるに越したことはありませんが,
人間ですから,思考が遠回りして
なかなか正解にたどり着かないことくらいあるでしょう。
しかし,問2において,安直に誤った合同条件を適用し,
$\rm\triangle ABD\equiv\triangle ACD\;$が示せたと主張する人は,
数学の指導をするべきではないと思います。
この質問に対するAIの回答や採点結果だけを見ても,
今回参加してもらっているチャットAIの多くは,
数学の相談相手として極めて不十分と言えそうです。
繰り返しますが,この問題は解けなくてもよいのです。
しかし,解けないなら解けないと
言ってくれないと困るのです。
誤った推論をさも正しいかのように主張し,
積極的に誤解を誘発する相手に,相談などできません。
分からないことは分からないと言う。
自分の解法が間違っていることに気づく。
間違っていると気づいたら,主張せず取り下げる。
それができないAIは,数学の相談相手としては
信用できないと言わざるをえないでしょう。
いずれはそのような最低限の行動が
安定してできるようになるのでしょうか?
今後のAIの進歩に期待したいと思います。
AIを批判する気はないけれども
筆者は,AI自体やAIの開発者を
批判するつもりは全くないのです。
成長途上のAIが避けて通れない道かもしれませんし,
もしそうなら仕方のないことですから。
ただ,これほど重大な欠陥を持つAIを
盲信してはいけないと,
利用者側に対して言いたいだけなのです。
そのためにはソフトな言い方をするわけにはいかず,
思ったことを思った通りに
述べる必要があると考えています。
ゆえにきつめの言い方になる部分もありますが,
ご理解いただければ幸いです。
次ページの内容
引き続き,問3にて検証を行います。
人間の作問者が陥りやすい間違いを,
AIが気づいて指摘してくれるのか?
という問題です。